
The 2021 Nobel Prize in Physics was announced this morning, “for groundbreaking contributions to our understanding of complex physical systems.” As often happens, this is to be split among three scientists for two different topics: half to Syukuro Manabe and Klaus Hasselmann “for the physical modelling of Earth's climate, quantifying variability and reliably predicting global warming,” and the other half to Giorgio Parisi “for the discovery of the interplay of disorder and fluctuations in physical systems from atomic to planetary scales.” What’s striking about this is that the two topics seem so very different.
As I have grumbled elsewhere, the unfortunate result of this Frankenprize (h/t Doug Natelson) is that the more complicated part is likely to be badly under-covered. We’re neck-deep in science reporters who have spent the last several years writing climate stories, which means it’s easy to fill column inches with explanations of the importance of Manabe’s and Hasselmann’s work. People who can talk sensibly about Parisi’s work, on the other hand, are not so common, and he’s likely to get somewhat short shrift as a result (to whatever degree your shrift can be shortened when you’ve just won half a Nobel, anyway...).
For that reason, I’m not going to talk about the climate piece at all; I’m confident that will be amply covered elsewhere. Instead, I’m going to try to give the clearest explanation I can of what Parisi won for, and why it matters more broadly than you might think.
Parisi, it should be noted, is a Name in several different areas of mathematical physics; my Twitter feed yesterday contained a lot of particle physicists cheering for his win because he’s one of the people behind an extremely important model for how quarks behave inside a nucleon. (I won’t attempt to explain that.) The work that the Nobel foundation specifically cited, though, was on “spin glasses,” a category of disordered materials, where Parisi made the crucial breakthrough that allowed models to be solved, and more importantly understood.
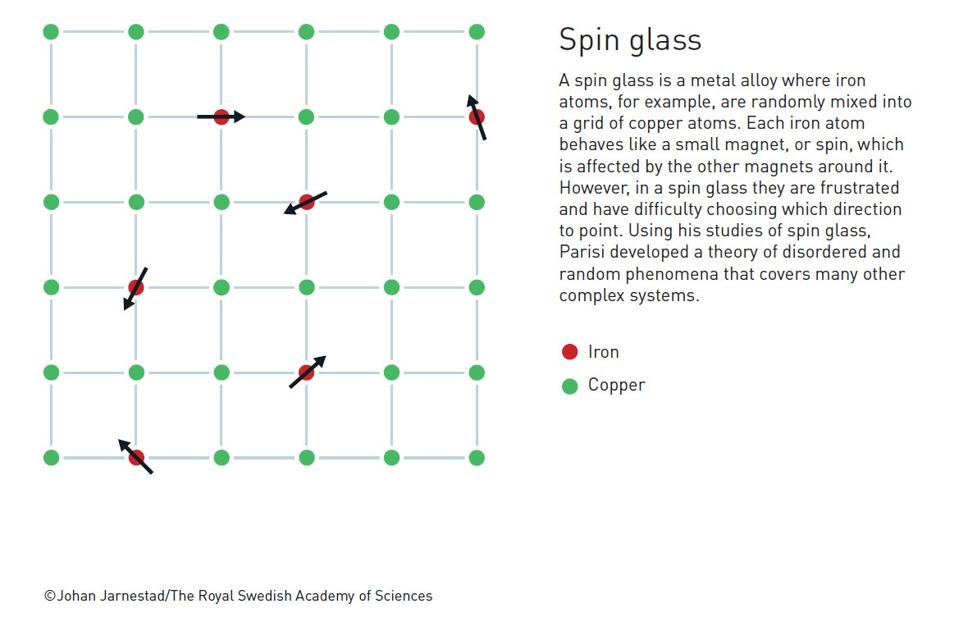
The classic example of a “spin glass,” used by the Nobel folks in citing Parisi’s work, is an alloy of non-magnetic metal with a small fraction of magnetic atoms mixed in. The energy of these atoms depends on the direction of their magnetic moment relative to the magnetic field created by all the other atoms— lower if aligned with the field, higher if opposite the field— and as always in physics and chemistry, the system will try to end up in the lowest energy state. These tend to be disordered— there isn’t a clear global pattern with all the magnets aligned in the same direction— which is where the “glass” part of the name comes from. In the same way that an amorphous solid like window glass doesn’t have an orderly crystal structure, a spin glass doesn’t have an orderly magnetic structure, but a bunch of little magnets in different places pointing in different directions. Despite the lack of order, though, these are remarkably resilient— again, much like regular glass— and the magnets aren’t readily re-oriented. The questions to ask are how to predict what configuration the system will land in, and how to understand why it’s so slow to change.
This is, as you might guess, an enormously complicated problem, but you can break it down to a toy model in which you consider the magnetic atoms as an array of quantum-mechanical spins, with each spin in the array coupled to some or all of the other spins in the array. If spin n and spin (n+1) are in the same direction, their energy increases slightly, say, but if they’re in opposite directions, it decreases by the same amount. The couplings are random, though, in both the size of the energy shift (reflecting the different distances between spins) and the direction (reflecting the different orientations)— that’s the crucial element of disorder.
This is a more complicated version of a method for modeling solids that dates back to the 1920’s, generally called an “Ising model” after Ernst Ising (I’m told that this is properly pronounced like “easing,” not “icing” as Americans tend to). If you make all the couplings the same, you get states that are relatively simple to calculate, but still show complex behavior depending on how many neighbors each spin has to interact with. A linear chain with nearest-neighbor interactions doesn’t do much, but a square array has a phase transition, an interaction strength where suddenly the whole system snaps into an ordered state, so these models are a huge part of courses in thermal and statistical physics.
Even the models with constant couplings can do weird things, though. If you put the spins in a triangular lattice with interactions set so each spin wants to be opposite its neighbors, you can create “frustration.” In a technical sense, not just among students assigned this as a homework problem— two of the three spins in a triangular cell can be made to point in opposite directions, but the third has to be the same as one of the others, and there’s no clear way to choose which. What happens in these frustrated spin lattices is a rich and interesting problem in its own right (and some folks in the cold-atom world are working on simulating them with Bose-Einstein condensates, a topic near to my heart).
Making the arrays bigger and expanding the range of the interactions makes this problem much harder to solve, and that’s even before you make the couplings random, as they are in real materials. When you try to extend this calculation to include disorder, you end up with a fiendishly difficult calculation when you try to compute the key quantities for predicting bulk properties of the system.
As often turns out to be the case, though, there’s One Weird Math Trick that makes the problem more tractable. You can simplify one of the most difficult steps by considering not a single configuration of spins, but a huge number of “replicas” of the system with the same disordered couplings, but potentially different individual spins. This might seem like it’s making things much worse by adding still more complexity, but as sometimes happens in math, writing the equations in these terms lets you re-arrange the resulting integrals in a way that makes them much easier to solve.
That lets you calculate an answer, but it’s maybe not immediately clear what it means. When you look carefully at the simplified equations, though, you find that one of the key quantities you end up calculating is essentially a measure of the similarity of two different “replicas.” So what this calculation is actually doing is, in a sense, identifying groups of very similar states within the vast number of possible replicas.

This is where Parisi’s key contribution comes in. The basic idea of the models and the introduction of disorder, and even the One Weird Trick of using replicas to simplify the calculation came from other people, but he realized the implications of the math. The business of identifying groups of similar states among the replicas allows you to identify and classify patterns within the replica space, imposing a kind of structure on the seemingly infinite range of possibilities. Parisi showed that this structure has a property called “ultrametricity,” which allows the configurations to be sorted in a way that’s hierachical, a bit like the tree diagram in the cartoon above.
This lets you understand conceptually what’s going on in the spin glasses. The exact configuration of the system in a low temperature state essentially settles into what you can think of as one of the lowest-level states of the tree, more or less at random. It can move between nearby states relatively easily, going up and back down one level, without needing much extra energy. Making a more significant change, though, requires going up the tree a ways and back down a different branch, which is much harder to do. That’s why the state is so resilient, despite lacking obvious order: making big changes in the magnetic order involves doing something complicated within the hierarchy of possible states, which takes energy. At low temperatures, these systems lock into one of a huge number of possible states with a particular energy, and they tend to stay close to that state, even though there may be other very different configurations available with the around the same energy, because the path to get there is difficult.
This might seem like just an elegant solution to a ridiculously abstract problem, but once you have the basic idea of using replicas to find structure in the states of a disordered system, you can apply it to lots of other situations, on a variety of scales. The tree-graph example should bring to mind things like neural and communications networks, and Parisi’s techniques have found applications there. You can cast some problems in granular materials in a similar mathematical form, and bring these same techniques to bear (indeed, compression of a box of particles is the other example given in the Nobel foundation’s popular explanation materials). As a number of people noted on Twitter, Parisi has also used this to explore the behavior of flocks of birds like starlings, where huge numbers of individual birds move in patterns that seem random and yet coordinated. Again, if you think about it, you can see how to map this onto the spin-glass problem: each bird adjusts its speed and direction depending on those of its neighbors, who are somewhat randomly distributed.

So, that’s what Parisi is being honored for. The original work was on a particular microscopic system of interest mostly to condensed matter physicists, but the central idea is extremely powerful, and applies on a wide range of scales, all the way up to weather and climate (though that connection is maybe a little strained). When you have a large number of things interacting with each other, and an element of disorder, Parisi’s replica symmetry breaking technique can often be used to predict aspects of the collective behavior. That’s the kind of deep and subtle insight that physicists seek and love to celebrate, and as such it’s richly deserving of at least half a Nobel Prize.
(Acknowledgement: I am indebted to Steve Thomson for a nice Twitter thread on this that helped clarify things, and to Thomson, Doug Natelson, and Magnus Borgh for checking a very sketchy outline of the above explanation for me. Whatever I got right, they helped with; anything I got wrong is my original contribution.)







