
In today’s article, you will learn about each of the greeks, their importance and how they impact option prices and strategies.
Whether you're a seasoned option trader looking to sharpen your skills or a newcomer eager to unlock the secrets of successful options trading, this article will equip you with the knowledge and tools you need.
The main options greeks are:
- Delta
- Gamma
- Vega
- Theta
- Rho
Delta
Delta measures the rate of change in an option's price given a $1 change in the underlying asset price.
Think of it as a gauge of how sensitive your option is to movements in the stock, index, or other underlying asset.
Delta values range from 0 to 1 for call options and from 0 to -1 for put options.
A call option with a Delta of 0.5 indicates that for every $1 increase in the underlying stock price, the option price is expected to increase by $0.50.
Conversely, a put option with a Delta of -0.5 suggests that for every $1 increase in the underlying stock price, the put option price is likely to decrease by $0.50.
Understanding Delta is crucial because it can provide insights into how an option will behave when the underlying asset moves.
A Delta of 1 means the option price moves in perfect harmony with the underlying asset.
If the stock goes up by $1, the call option price should increase by $1, all else being equal.
Delta Hedging
Delta hedging is a risk management technique commonly employed by option traders and market makers to neutralize or reduce directional risk in their portfolios.
It involves taking an offsetting position in the underlying asset, typically shares of stock, to balance the delta of an option position.
For instance, if an option trader is long a call option with a delta of +0.70, they would sell or short approximately 70 shares of the underlying stock to create a delta-neutral position.
By doing so, delta hedging aims to minimize potential losses resulting from adverse price movements in the underlying asset, providing traders with a more stable and predictable risk profile.
Gamma
Gamma measures the rate of change of Delta in response to a $1 movement in the underlying asset price.
An option with a gamma of +0.05 will see its delta increase by 0.05 for every $1 move in the underlying.
Likewise, an option with a gamma of -0.05 will see its delta decrease by 0.05 for every $1 move in the underlying.
Gamma is highest with short-dated options and at-the-money options.
For this reason, the last week of an options life is referred to as “gamma week”.
A lot of traders do not want to be short gamma during gamma week.
Net sellers of options will be short gamma and net buyers of options will be long gamma.
This makes sense because most sellers of options do not want the stock to make a big move, while buyers of options benefit from large movements.
A larger gamma (positive or negative) leads to a larger change in delta when your stock moves.
Low gamma positions display a flatter risk graph, reflecting less fluctuation in P&L.
High gamma positions display a steeper risk graph, reflecting high fluctuation in P&L.
Vega
Vega measures an option's sensitivity to changes in implied volatility.
When implied volatility rises, options tend to become more expensive because there is a greater likelihood of significant price movements.
Let’s look at a stock priced at 50. Consider a 6-month call option with a strike price of 50:
If the implied volatility is 90, the option might be $12.50
If the implied volatility is 50, the option might be $7.25
If the implied volatility is 30, the option might be $4.50
Vega tells us how much an option price might change for a one percent change in implied volatility.
For instance, if an option has a Vega of 0.30, it implies that if implied volatility increases by 1%, the option price will increase by $0.30, assuming all other factors remain constant.
Understanding Vega is crucial for managing risk, especially when trading multiple option strategies.
A good idea is to trade a combination of short Vega and long Vega strategies.
Short Vega strategies include Short Straddles, Short Strangles, Butterflies, Iron Condors and Credit Spreads.
Long Vega Strategies include Long Straddles, Long Strangles, Calendar Spreads and Debit Spreads.
Theta
Theta measures how an option’s price changes with the passage of time. It tells you how much an option’s price will decrease with the passage of one day.
For example, if an option has a Theta of -0.05, it means the option's price will drop by $5 per day, all else being equal.
A positive Theta value means the option position will benefit from time decay.
A negative Theta value means the option position will lose money from time decay.
One of the characteristics of options is that they have a limited existence as they are contracts which contain a beginning and an expiration date.
As the expiration date of the options contract approaches, the value of the contract will change more dramatically.
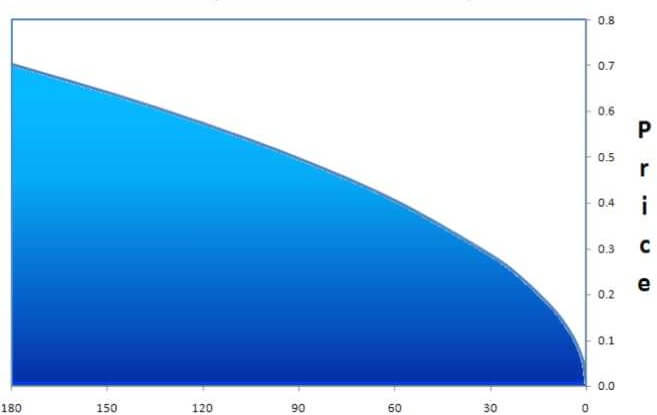
For buyers of options, Theta represents a daily cost that must be overcome by price movement or changes in other Greeks to achieve profitability.
Options sellers aim to profit from time decay while trying not to suffer negative impacts from other greeks.
Strategies that benefit from time decay include Short Straddles, Short Strangles, Butterflies, Calendar Spreads, Iron Condors and Credit Spreads.
A common misconception among beginner traders is that they think they can sell options on Friday, and buy them back cheaper on Monday.
In reality, the weekend has already been priced into option values as early as Thursday afternoon.
Rho
Rho measures how much an option's price is expected to change with a 1% change in interest rates.
Rho is more relevant to traders of long-term options and less relevant for short-term options.
Rho is positive for call options and negative for put options.
This means that call option premiums tend to increase when interest rates rise, while put option premiums decrease.
In practice, Rho's impact is generally less significant than Delta or Theta for many options traders.
However, it has become more relevant in recent years given the significant changes in interest rates.
Understanding and harnessing the power of option Greeks can significantly elevate your options trading game.
Delta, Gamma, Theta, Vega, and Rho are not just abstract concepts; they are powerful tools that can guide your decisions, manage risk, and optimize profitability.
As you navigate the dynamic landscape of the financial markets, a mastery of these Greeks opens the door to a strategic and informed approach.
So, embrace the knowledge, apply it to your trades, and embark on a journey where the complexities of options become stepping stones to success.
On the date of publication, Gavin McMaster did not have (either directly or indirectly) positions in any of the securities mentioned in this article. All information and data in this article is solely for informational purposes. For more information please view the Barchart Disclosure Policy here.






