
What if Pi Day, perhaps the best known mathematical holiday, was actually better celebrated in the summer?
Currently falling on March 14 — 3/14, in honor of the first three digits of the infamous irrational number — Pi Day celebrates what is often the first irrational number grade school students meet. However, one mathematician says it ought to fall on July 22.
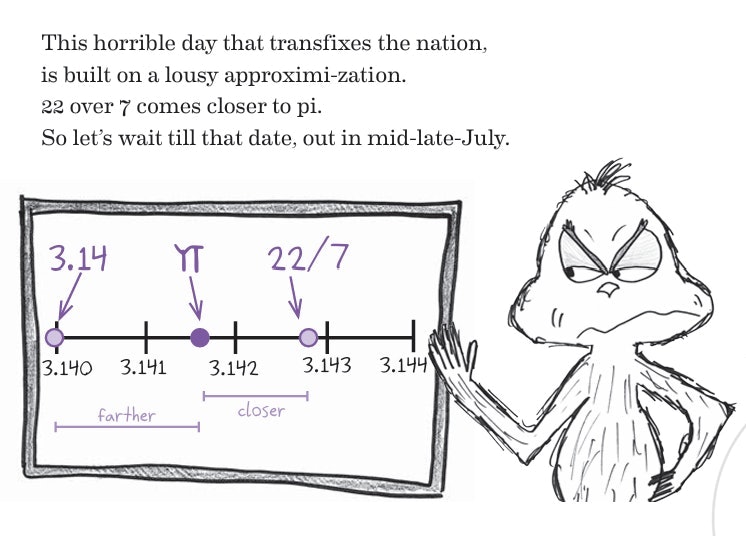
22/7 (as in the 22nd of July, the way most of Europe represents dates) is pi in fraction form. On a number line, if you pin up 3.14, pi, and 22/7, pi is just ever so slightly closer to 22/7 than to 3.14, making the fraction the superior approximation. So, if you want to be a pedantic stickler about your math holidays, then start celebrating Pi Day in July.
Ben Orlin, in his new book Math for English Majors (out September 3), explores pi and other mathematical concepts for those who haven’t found themselves to be mathematically minded. We live in a world that increasingly foists mathematics upon us either in the form of financial literacy or artificial intelligence. Understanding or even simply enjoying math can help ease this inevitable, beautiful part of life.
This interview has been edited and condensed for clarity.
Inverse: First of all, what is pi and what makes it so important in mathematics?
Ben Orlin: Pi is a beautiful number that, in its simplest form, is the ratio of a circle’s circumference to its diameter. The distance around the outside will be much further than the distance across it. It's a little more than three times as far, and the exact number is pi.
The moment you have a circle, you can't get away from pi. What do you want to know about the circle? You probably want to know how far across it is, you probably want to know how far around is the outside, and you might want to know how much area it covers. To express any of those things, you need pi. One of the things mathematicians study a lot is any kind of repeating and cyclic behavior, which is any kind of cycle in nature involving circles in disguise. This includes waves or periodicity or repetition also involves pi, because there are these hidden circles.
Waves are probably the most ubiquitous example. We communicate with sound waves, we see with light waves. And waves are circles unraveled. Mathematicians think a lot about the logical order in which we can construct objects mathematically. Imagine the hand of a clock, rotating as it goes around the circle. What you can do is track how high up that point is that it's pointing at. So ignore where it is left and right on the clock, just look at how high it is up and down. You watch as the clock rotates, it goes up to the top and then it descends down again, and then it goes down below where it originally was and then it comes back up. And then this will keep happening again and again. Where you're looking at will rise and fall and rise and fall. And you get a sine wave. That's the basic shape of every wave that we see in nature, including music notes and light moving through space.

Is 3.14 actually the best way to express pi? If not, what is?
We have these languages for talking about in between numbers like fractions and decimals but neither one can quite express pi exactly. Pi is not 22/7, but pi is also not 3.14. Both of those are wrong. But technically, 22/7 is just a tiny bit less wrong.
If you look on a number line, pi’s just about halfway between 3.14 and 22/7, but leaning a little bit closer to 22/7. So that's a more convenient way to do it. It is also a much older way to think about pi. Decimals are a pretty recent mathematical invention in the scheme of things, whereas fractions are the way that people have thought about mathematics as long as we've had mathematics.
What are your thoughts on Pi Day?
I love Pi Day. It's this bizarre math appreciation day. In 1988, this physicist at the science museum in San Francisco, Larry Shaw, came up with this bizarre set of associations and connections and puns. That crystallized into this beautiful holiday that spread worldwide. Beneath the puns and the wordplay, and the silly celebration, though, is unshakeable mathematics. It can take a while to access those ideas — you have to pass through this layer of language. But once you get down into that subterranean level, it's fun, and you can see the connectedness of things in a way that isn't otherwise possible.
This is your fourth book about math. What’s different about it? What do you hope readers get out of it?
In my career as a teacher and a writer, I have met hundreds — maybe more than hundreds — of people who self identify as not-a-math-person. Math just turns them off, for whatever reason. I wanted to write something that was just a little package of all the things I wish I could say to them.
In the others, I tried to push as far away as I could from school math. I was very careful to pick ideas that I thought you could express in plain English. And that's nice, but it sort of sidesteps what turns people off about math. What I hope people get out of it is a sense that math is a language. To learn it, you have to do this strange dance where you hop back and forth between the ideas and the language, because it's hard to express the ideas without the language. But the structure of the language doesn't make any sense, unless you have some experience of those ideas. The book does that dance back and forth a lot. I'm sort of trying to teach the choreography.
What makes pi crucial to enjoying math for non-math people?
It's your first encounter with an irrational number. Once you become a jaded, experienced mathematician, irrational numbers stop feeling quite so special. If you could stretch out a number line and throw a dart at it, the dart would be virtually guaranteed to hit an irrational number. But I like seeing it with beginner's eyes. And with beginner's eyes, it's bizarre. It's the first number you've met that has this bizarre property. It's an unspeakable number. Pi itself just leans away from us. It just keeps escaping. Math is full of that, but it's very hard to get to the rest of them in math. Pi is the one that younger people and beginners and outsiders can access.
What do we still not understand about pi?
In terms of measurement, we get it pretty well. We've got it down to trillions of digits. But how the number relates to other numbers, there are actually some surprising open questions. For example, if you combine pi and e. Pi comes out of circles; e comes out of exponential growth. We all but know that pi raised to the e power or e to the pi power, we're very confident that's irrational. But there's actually a chance that it isn't. We haven't proven that it's irrational, because these numbers are very hard to get a handle on. And so there's some very simple questions about pi and e in particular that remain unanswered.







